힙 정렬

힙(Heap)이란?

힙 정렬은 Heap이라는 자료구조를 이용한 정렬 알고리즘입니다. 힙에는 최소 힙(min heap)과 최대 힙(max heap)이 있는데, 이들은 값이 저장되는 방향만 반대일 뿐 성질은 동일합니다.

이때 힙(heap)은 complete binary tree를 기반으로 한 자료구조로, 다음의 힙 성질(heap property)을 만족합니다:

• min-heap property: 각 노드의 값은 자기 자식의 값보다 작거나 같습니다.
• max-heap property: 각 노드의 값은 자기 자식의 값보다 크거나 같습니다.

leaf 노드는 자식이 없으므로 논리상 이 성질을 자동으로 만족하게 됩니다. 모든 노드가 위 성질을 만족하면, min heap의 경우 root에는 최솟값이 자리하게 되고, max heap의 경우 최대값이 자리하게 됩니다. 이 포스트에선 min heap을 기준으로 설명하겠습니다.

개념

힙 정렬은 우선 주어진 배열을 힙으로 만듭니다(heapify). 그런 다음, 힙에서 가장 작은 값을 차례로 하나씩 제거하면서 힙의 크기를 줄여나갑니다. 이렇게 하면 마지막에는 힙에 아무 원소도 남지 않게 되는데, 이 경우 힙 정렬 과정이 완료됩니다.

우선 주어진 배열을 힙으로 만드는 과정, 힙에서 최소 원소를 제거하고 나서도 heap property를 만족하도록 힙을 “수선” 하는 과정을 살펴봅시다.

힙 만들기

일반적으로 트리를 표현할 때는 포인터 등을 이용하여 구현할 수도 있으나, complete binary tree이기 때문에 그렇게 하지 않고도 간단하게 구현할 수 있습니다. 아래 그림은 배열을 통해 최소 힙을 표현한 예시입니다:

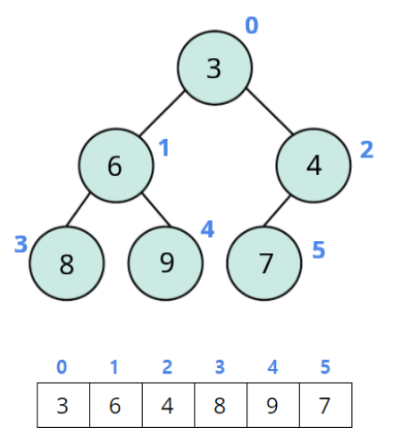
일반적으로 A[i]의 자식은 왼쪽, 오른쪽 각각 A[2i + 1], A[2i + 2]가 됩니다. 또한, A[i]의 부모는 A[⌊(i-1)/2⌋]가 됩니다. 이렇게 배열의 인덱스를 이용하여 부모·자식 간의 관계를 간단하게 계산할 수 있으므로 따로 포인터 등을 이용하여 구현할 필요가 없는 것이죠!

이제 정렬하고자 하는 n개의 원소를 가진 배열 A[0 ⋯ n-1]이 있다고 해봅시다. 위 그림과 같이 이 배열을 complete binary tree로 해석할 수 있지만, 각각의 값들이 힙 성질을 만족하지 않고 제멋대로 들어 있다고 한다면, 이 배열이 힙 성질을 만족하도록 요소들을 재배치해서 힙으로 만들어야 합니다. 이 과정을 그림으로 나타내면 다음과 같습니다:

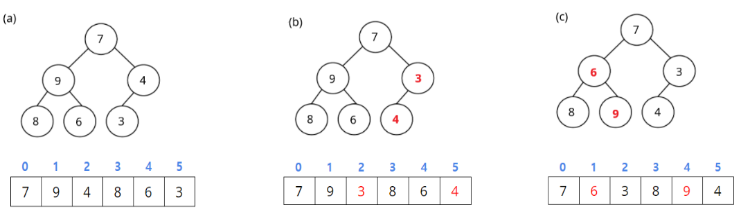
• (a): 초기에 주어진 배열로, 배열의 원소들이 아무렇게나 들어있는 상태입니다.
• (b): 맨 뒤에서부터 시작하여, (최소)힙 성질을 만족하지 않는 첫 번째 원소 A[2]를 체크합니다. 부모와 자식의 값이 힙 성질을 만족하지 않으므로 A[2]와 A[5]를 스왑합니다.
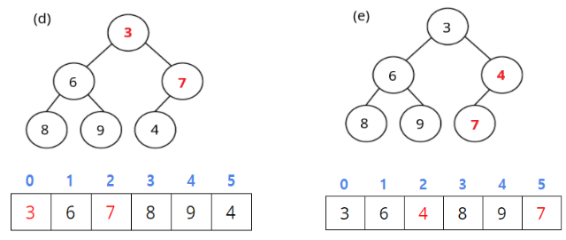
• (c): 힙 성질을 만족하지 않는 두 번째 원소인 A[1]을 체크합니다. 두 자식 A[3], A[4]중 작은 값인 6보다 크므로 이 둘을 스왑합니다.
• (d): 힙 성질을 만족하지 않는 세 번째 원소인 A[0]을 체크하여 두 자식 중 작은 값인 3과 스왑합니다
• (e): 방금 교환해서 A[2]로 내려온 7이 자식의 값 4보다 크므로 둘을 스왑합니다.

아래 수도 코드는 배열 A[0 ⋯ n-1]을 입력으로 받아 힙을 만드는 알고리즘입니다. heapify(A, k, n)은 k 밑에 있는 두 서브 트리가 힙 성질을 만족하는 상태에서 k를 루트로 하는 트리가 힙 성질을 만족하도록 수정하는 함수입니다.

buildHeap(A, n) {    // A[0 ⋯ n-1]을 힙으로 만듦.
  for i from floor(n / 2) down to 0:
    heapify(A, i, n);
}

// A[k]를 루트로 하는 트리를 힙 성질을 만족하도록 수정한다.
// A[k]의 두 자식을 루트로 하는 서브 트리는 힙 성질을 만족한다.
// n은 최대 인덱스를 나타낸다 (전체 배열의 크기).
heapify(A, k, n) {
  left = 2k + 1;
  right = 2k + 2;

  if (right < n):    // k가 두 자식을 가지는 경우.
    if (A[left] < A[right]): smaller = left;
    else: smaller = right;

  else if (left < n):    // k가 왼쪽 자식만 가지는 경우.
    smaller = left;

  else: return;    // k가 리프 노드이므로 종료.

  // 재귀적 조정. 즉, k와 smaller를 바꾼 다음
  // smaller를 루트로 했을 때에도 힙 성질을 만족하는지 체크.
  if (A[smaller] < A[k]):
    swap(A[k], A[smaller]);
    heapify(A, smaller, n);
}

leaf는 그 자체로 힙 성질을 만족하므로, buildHeap()은 leaf가 아닌 노드 중 맨 뒤에서부터 루트로 삼아 heapify()를 수행합니다. 즉, 위 코드에서 ⌊n/2⌋는 leaf가 아닌 노드 중 맨 마지막 노드의 인덱스를 나타냅니다.

A[⌊n/2⌋]부터 A[0]까지 차례로 루트로 삼아 총 $⌊\frac{n}{2}⌋ + 1$번의 heapify()를 수행하고 나면 A[0 ⋯ n-1]는 힙 성질을 만족하게 됩니다.

buildHeap의 수행시간을 살펴봅시다. 우선, heapify(A, k, n)함수는 k를 루트로 하는 트리의 높이가 시간을 좌우하는데, 어떠한 이진 트리도 높이가 $log_{2}n$을 넘지 않으므로 heapify를 한 번 수행하는데 O(logn)이 소요됩니다. 따라서 buildHeap에서 heapify를 호출하는 횟수는 ⌊n/2⌋이므로, 전체적으로 O(nlogn)이 소요된다고 할 수 있습니다.

하지만 이것은 다소 과하게 잡은 상한인데, 모든 heapify가 O(logn)만큼 걸린다고 보는 것은 과하다고 할 수 있습니다. 그 이유는, 맨 처음에 호출되는 heapify의 트리의 높이는 1이고, 이렇게 높이가 1인 트리가 여러 개 존재합니다. 그다음 레벨로(즉, 위로) 올라가면 높이가 2인 트리들을 만나게 되는데, 높이가 2인 트리의 개수는 높이가 1인 트리의 개수보다 적습니다. 이런 식으로 위로 올라갈수록 높이가 높은 트리의 수가 줄어들게 되는데, 이를 합산하면 O(nlogn)이 아닌 Θ(n)이 됩니다.

정렬

heapify를 통해 힙이 완성되었다면 이를 기반으로 정렬을 수행할 차례입니다. 루트 노드를 맨 마지막 노드와 스왑하고, 힙의 크기를 1만큼 줄여 heapify를 실행하는 과정을 반복하면 정렬된 배열을 얻을 수 있습니다:

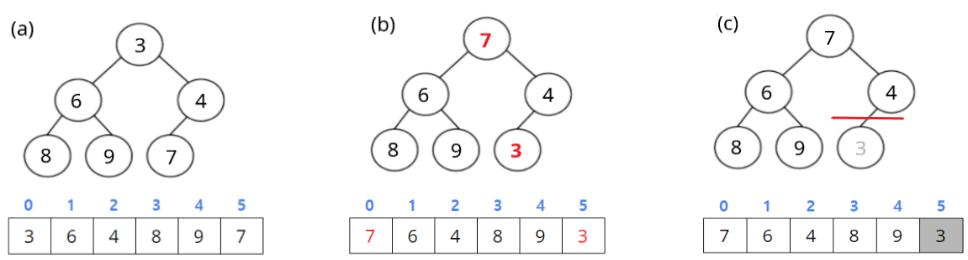
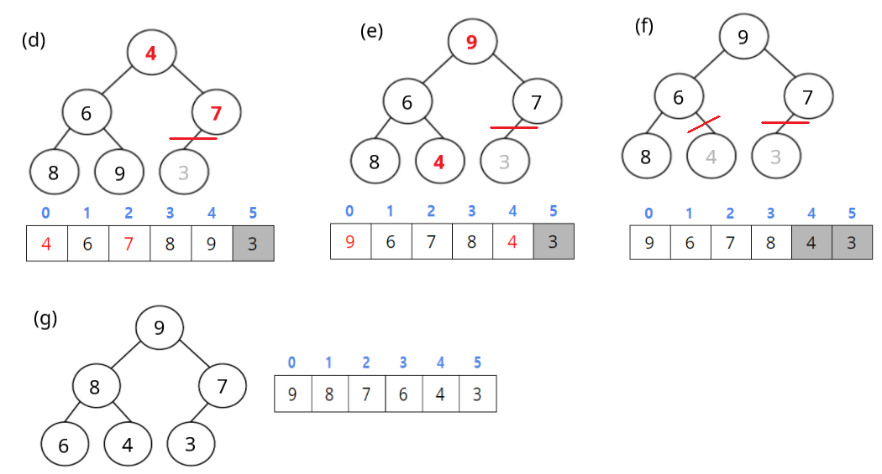
• (a): heapify를 통해 만들어진 배열입니다.
• (b): root와 맨 마지막 원소를 스왑합니다.
• (c) ~ (d): heap의 크기를 하나 줄이고, 줄어든 heap에 대해 heapify를 수행합니다.
• (e): (b)에서와 같이, root와 맨 마지막 원소를 스왑합니다.
• (f): (c) ~ (d)에서와 같이, heap의 크기를 하나 줄이고, 줄어든 heap에 대해 heapify를 수행합니다.
• (g): 위 과정들을 반복하면 최종적으로 정렬된 배열을 얻을 수 있습니다.

최종적인 힙 정렬에 대한 수도코드는 다음과 같습니다:

heapSort(A, n) {   // A[0 ⋯ n-1]을 정렬한다.
  buildHeap(A, n);
  for i from n - 1 down to 0:
    swap(A[0], A[i]);
    heapify(A, 0, i);
}

힙 정렬의 수행 시간을 살펴보자면 우선, buildHeap은 Θ(n)만큼의 시간이 걸립니다. heapSort의 for루프는 n-1번 순환하고, 각 순환에서 시간을 좌우하는 heapify는 O(logn)이 걸리므로 힙 정렬의 총 수행시간은 O(nlogn)이 됩니다.

자바스크립트 구현

min heap을 이용한 내림차순 정렬:

function heapSort(A, n) {
	buildHeap(A, n);
	for (let i = n - 1; i > 0; i--) {
		[A[0], A[i]] = [A[i], A[0]];
		heapify(A, 0, i);
	}
}

function buildHeap(A, n) {
	for (let i = Math.floor(n / 2); i >= 0; i--) {
		heapify(A, i, n);
	}
}

function heapify(A, root, n) {
	let left = 2 * root + 1;
	let right = 2 * root + 2;
	let smaller = root;

	if (right < n) smaller = A[left] < A[right] ? left : right;
	else if (left < n) smaller = left;
	else return;

	if (A[smaller] < A[root]) {
		[A[smaller], A[root]] = [A[root], A[smaller]];
		heapify(A, smaller, n);
	}
}

let a = [7, 9, 4, 8, 6, 3];
heapSort(a, a.length);
console.log(a); // [ 9, 8, 7, 6, 4, 3 ]

max heap을 이용한 오름차순 정렬:

function heapSort(A, n) {
	buildHeap(A, n);
	for (let i = n - 1; i > 0; i--) {
		[A[0], A[i]] = [A[i], A[0]];
		heapify(A, 0, i);
	}
}

function buildHeap(A, n) {
	for (let i = Math.floor(n / 2); i >= 0; i--) {
		heapify(A, i, n);
	}
}

function heapify(A, root, n) {
	let left = 2 * root + 1;
	let right = 2 * root + 2;
	let larger = root;

	if (right < n) larger = A[left] > A[right] ? left : right;
	else if (left < n) larger = left;
	else return;

	if (A[larger] > A[root]) {
		[A[larger], A[root]] = [A[root], A[larger]];
		heapify(A, larger, n);
	}
}

let a = [7, 9, 4, 8, 6, 3];
heapSort(a, a.length);
console.log(a); // [ 3, 4, 6, 7, 8, 9 ]

REFERENCE

• 쉽게 배우는 알고리즘 - 문병로