자바스크립트 MAX_SAFE_INTEGER와 MAX_VALUE

카테고리: JavaScript

January 04, 2022

IEEE 754에 대해 잘 모르시는 분들은 컴퓨터는 어떻게 숫자를 표현하는가를 보고 오시는 것을 추천합니다!

Number.MAX_SAFE_INTEGER

우선, 자바스크립트에서 “안전”하게 정수를 표현할 수 있는 최대값이 왜 9007199254740991 ( $2^{53}-1$ )인가에 대해 알아봅시다. 이때 “안전”하다는 말은 정수를 정확하게 나타낼 수 있고, 올바르게 값을 비교할 수 있다는 의미입니다.

다들 아시다시피 자바스크립트의 Number 타입은 IEEE 754 Double Precision 형식을 사용하여 숫자를 나타냅니다. 이때 mantissa가 최대 52비트 이므로 정수를 “안전”하게 표현할 수 있는 최대값은 이 mantissa가 모두 1로 채워진 경우입니다. 이를 정규화된 형식으로 표현하면:

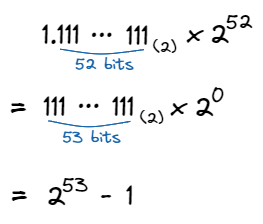
JavaScript max safe integer — MAX_SAFE_INTEGER 값을 구하는 과정

위 그림과 같은 방식으로 추론하면 왜 MAX_SAFE_INTEGER 값이 ( $2^{53}-1$ )인지 알 수 있습니다.

그럼 MAX_SAFE_INTEGER 값에 1을 더하면 어떻게 될까요?

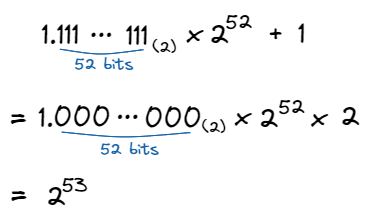
JavaScript max safe integer plus one — MAX_SAFE_INTEGER + 1

위와 같이, 모든 mantissa의 수가 자리올림 되어 0으로 바뀌고 exponent가 52에서 53으로 증가하게 됩니다. 따라서 MAX_SAFE_INTEGER + 1의 값은 $2^{53}$ 이 되는 것이죠.

하지만 이제부터 재미있는 일이 일어나기 시작합니다. MAX_SAFE_INTEGER + 1보다 큰 값은 2씩 증가하고, 홀수는 표현할 수 없게 되는 것이죠:

input: 9007199254740992 + 1  output: 9007199254740992  // expected: 9007199254740993
input: 9007199254740992 + 2  output: 9007199254740994  // expected: 9007199254740994
input: 9007199254740992 + 3  output: 9007199254740996  // expected: 9007199254740995
input: 9007199254740992 + 4  output: 9007199254740996  // expected: 9007199254740996

이는 다음 그림을 통해 설명할 수 있습니다:

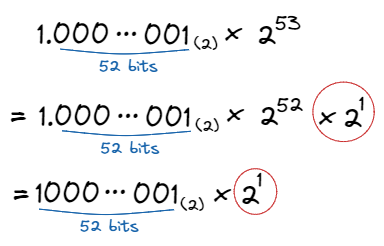
JavaScript larger than max safe integer plus one — MAX_SAFE_INTEGER + 1 보다 큰 수

위 그림처럼, MAX_SAFE_INTEGER + 1 보다 큰 수는 exponent값이 53 이상이므로 소수점을 (mantissa의) 52비트 만큼 이동시키고 나서도 여분의 2의 제곱꼴이 남아있게 됩니다. 이 때문에 1을 더한다고 해도 남아있는 2의 제곱꼴로 인해 실제론 2의 제곱꼴씩 증가하게 되는 것이죠.

위 그림에선 2가 남아있게 되었지만 수가 더욱 커지면 $2^2$ , $2^3$ 등의 수가 남아있게 됩니다. 예를 들어 9,007,199,254,740,992 * 2 = 18,014,398,509,481,984보다 큰 수의 경우 $2^2$ 가 남아있게 되어 수가 4씩 증가함을 알 수 있습니다:

input: 18014398509481984 + 1  output: 18014398509481984  // expected: 18014398509481985
input: 18014398509481984 + 2  output: 18014398509481984  // expected: 18014398509481986
input: 18014398509481984 + 3  output: 18014398509481984  // expected: 18014398509481987
input: 18014398509481984 + 4  output: 18014398509481988  // expected: 18014398509481988

Number.MAX_VALUE

MAX_VALUE의 경우도 비슷합니다. mantissa 52비트 모두를 1로 채우고, exponent의 최대값인 *1023을 적용하면 double precision으로 표현할 수 있는 최대값인 1.7976931348623157e+308 (= $2^{1024}-1$ )가 됩니다.

*double precision에서 exponent의 최대값이 1023인 이유는, exponent 11비트 모두 1인 경우 (즉, 1024) 특수값으로 취급되므로 $(2^{11}-1)-1 = 1023$ 이 됩니다.

음수의 경우, 부호 비트만 다르고 이와 동일한 논리가 적용됩니다.

References

What is JavaScript’s highest integer value that a number can go to without losing precision? - stackoverflow

Number.MAX_SAFE_INTEGER - MDN

Number.MAX_VALUE - MDN