컴퓨터는 어떻게 숫자를 표현하는가

카테고리: Computer Architecture

January 03, 2022

정수 표현

이진수로 표현

우리 인간은 10진법을 사용하여 수를 표현합니다. 가령, 987은 9가 100개, 8이 10개, 7이 1개 있다는 것을 의미하죠.

혹은, 정수를 다음과 같이 표기할 수도 있습니다:

$278 = (2 × 10^2) + (7 × 10^1) + (8 × 10^0) = 200 + 70 + 8$

이진수도 위와 비슷한 방법으로 표현할 수 있죠:

$1101_2 = (1 × 2^3) + (1 × 2^2) + (0 × 2^1) + (1 × 2^0) = 8 + 4 + 0 + 1 = 13$

물론 분수를 표현하는 것도 가능합니다:

$1.101_2 = (1 × 2^0) + (1 × 2^{-1}) + (0 × 2^{-2}) + (1 × 2^{-3}) = 1 + 1/2 + 0 + 1/8 = 1.625$

16진수로 표현

위와 같이 이진수로 수를 표현하다 보면 그 길이가 너무 길어지는 경우가 있기 때문에, 흔히 16진수를 많이 사용합니다. 또한, 이진수를 10진수로 변환하는 것보다 16진수를 10진수로 변환하는 것이 편한 이유도 있습니다.

16진수는 총 16자리를 표현해야 하므로, 0~9 뿐만 아니라 추가로 알파벳 A, B, C, D, E, F를 이용하여 각각 10, 11, 12, 13, 14, 15를 나타냅니다. 수를 나타내는 기본적인 방법은 이진수와 동일합니다:

$13_{16} = (1 × 16^1) + (3 × 16^0) = 16 + 3 = 19$

$1AD = (1 × 16^2) + (10 × 16^1) + (13 × 16^0) = 256 + 160 + 13 = 429$

그리고, 흔히 16진수를 표현할 때 접두사로 0x를 많이 사용합니다. 예를 들면, 1AD = 0x1AD, FF = 0xFF와 같이요. 또, $2^4 = 16$ 이므로, 16진수 한 자리를 4비트로 볼 수 있습니다. 이를 이용하면 16진수를 10진수로 쉽게 변환할 수 있습니다.

음수를 포함한 정수 표현 방법

대부분의 컴퓨터 시스템에서, 일반적으로 정수는 4바이트로 표현됩니다. 총 32비트 중에, 최상위비트(Most Significant Bit, MSB)는 부호를 나타내기 위해 사용되는데, 이를 부호 비트(sign bit)라고 합니다. 부호 비트가 0이면 양수, 부호 비트가 1이면 음수입니다.

양수(부호 비트가 0)를 표현할 땐 위에서 살펴본 것과 같이 이진수 그대로 표현하면 됩니다:

0101 0100 1101 1010 0100 0001 0111 0001₂ = 0x54DA 4171 = 1,423,589,745

0000 0000 0000 0000 0000 0000 0000 1000₂ = 0x00000008 = 8

음수(부호 비트가 1)를 표현하는 데엔 크게 3가지 방법이 존재합니다:

Sign and magnitude: MSB를 제외한 나머지 비트가 해당 음수의 절대값을 나타냅니다. 예를 들어, 1001₂ = -1, 1011₂ = -3 입니다. 이는 꽤 직관적인 방법이지만 다음과 같은 단점이 존재합니다:
1. 0을 표현하는데 두 가지 방법이 존재하게 됩니다. 예를 들면, 0000₂ = 0, 1000₂ = -0 입니다.
2. 덧셈과 뺄셈 연산을 부호에 따라 서로 다르게 처리해줘야 합니다.
1’s Complement: 1의 보수를 사용하여 음수를 표현하는 방법입니다. 즉, 부호 비트가 1일 때, 해당 이진수의 1의 보수를 취한 값이 음수의 절대값이 됩니다. 0에 대한 1의 보수는 1이고, 1에 대한 1의 보수는 0입니다. 예를 들어, 11010100₂의 1의 보수는 00101011₂ = 43 이므로 11010100₂ = -43이 됩니다. 하지만 이 방법도 sign and magnitude와 같은 단점이 존재합니다.
2’s Complement: 2의 보수를 사용하여 음수를 표현하는 방법입니다. 이때 2의 보수는 1의 보수에 1을 더하여 구합니다. 예를 들어, 11010100₂의 2의 보수는 00101100₂ = 44 이므로 11010100₂ = -44가 됩니다. 대부분의 현대 컴퓨터 시스템은 2의 보수법을 사용하는데, 그 이유는
1. 0을 표현하는 방법이 오직 하나 존재하고,
2. 덧셈과 뺄셈을 할 때 부호에 따라 다르게 처리해줄 필요가 없고,
3. 덧셈 로직을 이용하여 뺄셈을 수행할 수 있기 때문입니다.

n비트를 사용한 정수 표현방법 비교

표현방법	표현범위	나타낼 수 있는 수의 개수
Sign Magnitude	-2^n-1+1 ~ 2^n-1-1	2^n-1
One’s Complement	-2^n-1+1 ~ 2^n-1-1	2^n-1
Two’s Complement	-2^n-1 ~ 2^n-1-1	2ⁿ

Integer Overflow

산술 연산의 결과가 해당 비트로 표현할 수 있는 범위를 넘어서는 것을 overflow라고 합니다. overflow에는 최대값을 넘어서는 overflow와 최소값을 넘어서는 overflow가 있습니다.

overflow가 발생하게 되면 프로그램이 예기치 못한 동작을 할 수 있으므로 주의해야 합니다. 32비트의 예를 들면 다음과 같습니다:

0111 1111 1111 1111 1111 1111 1111 1111₂ (2147483647) + 1
= 1000 0000 0000 0000 0000 0000 0000 0000₂ (-2147483648)

1000 0000 0000 0000 0000 0000 0000 0000₂ (-2147483648) - 1
= 0111 1111 1111 1111 1111 1111 1111 1111₂ (2147483647)

실수 표현

실수를 표현하는 방법을 알아보기 전에, 컴퓨터에서 실수를 완벽하게 표현할 수 없다는 점을 알아둬야 합니다. 정수는 정해진 범위 안에서는 그 값을 정확하게 나타낼 수 있지만, 실수는 임의의 두 실수 사이에 무한히 많은 실수가 존재하기 때문에 컴퓨터에서 실수를 정확하게 표현할 수 없습니다 (예를 들면, 정수는 1 다음에 2이지만, 실수는 1.0 다음에 2.0이라고 할 수 있을까요? 1.0 다음엔 1.1이지 않을까요? 아니면 1.01? 혹시 1.00000000…1? 🤔).

실수를 표현하는데 크게 두 가지 방법을 고려해볼 수 있습니다:

고정 소수점(fixed point) 방식: 소수점을 어느 특정 위치에 고정하고 소수점 앞부분은 실수의 정수 부분을, 소수점 뒷부분은 실수의 소수 부분을 나타내도록 하는 방식입니다. 예를 들어, 8비트로 실수를 표현한다고 가정하면 첫 4비트는 정수를, 뒤 4비트는 소수를 나타내도록 할 수 있습니다. 이를 이용하면 1010.0111₂는 1010 0111로 나타낼 수 있고 11.011₂는 0011 0110으로 나타낼 수 있습니다. 이는 근본적으로 정수 표현법과 크게 다르지 않으므로 구현이 간단하다는 장점이 있지만, 표현할 수 있는 수의 범위가 제한된다는 단점이 있습니다. 따라서 이러한 방식은 임베디드 시스템과 같이 단순함이 중요한 곳에서만 사용됩니다.
부동 소수점(floating point) 방식: 고정 소수점과는 달리, 부동 소수점 방식은 말 그대로 소수점이 “떠다닙니다”. 부동 소수점 방식은 대게 과학적 표기법으로 나타내는데, 소수부(fraction)를 F, 지수부(exponent)를 E, 기수(radix)를 r이라고 한다면 실수를 $F × r^E$ 와 같이 나타냅니다. 예를 들면, $123.456$ 을 $1.23456 × 10^2$ 와 같이 나타낼 수 있습니다.

현대 컴퓨터는 실수를 표현할 때 IEEE 754 표준을 사용하여 나타냅니다. 여기에는 32비트 표현법(single precision)과 64비트 표현법(double precision)이 있습니다.

앞서 말했듯이, 정수와 달리 실수를 정확하게 표현하는 것은 불가능하므로 실수를 표현할 때 해당 실수와 가장 가까운 수를 근사(approximate)하여 나타내게 되는데, 이로 인해 정밀도 문제(loss of precision)가 발생할 수 있습니다.

IEEE 754 표준을 이용한 실수 표현

IEEE 754에는 3가지 기본 요소가 존재합니다:
1. 부호: 0은 양수를, 1은 음수를 나타냅니다.
2. Biased exponent: 지수부(exponent)는 양의 지수 $x^n$ 와 음의 지수 $x^{-n}$ 모두를 표현할 수 있어야 합니다. 이를 위해 비트로 표현된 지수값에 bias를 빼서 실제 지수값을 구합니다. $k$ 를 지수부의 비트수라고 하면 bias는 $2^{k-1}-1$ 이 됩니다. 지수가 8비트이면 bias는 $2^{8-1}-1 = 127$ 이고, 지수가 11비트이면 bias는 $2^{11-1}-1 = 1023$ 입니다. 이때 지수부를 bias 시키는 이유는 양의 지수( $x^n$ )와 음의 지수( $x^{-n}$ )를 같이 표기하기 위해선 지수부의 값에 부호가 존재해야 하는데, 흔히 사용하는 2의 보수법을 이용하면 수를 비교하기가 힘들어지기 때문에 이와 같은 방식을 사용합니다. 따라서 실질적으로 저장할 땐 비교의 편의성을 위해 unsigned 형식으로 저장하고, 이후 값을 해석할 땐 저장된 값에 bias를 빼서 해석합니다.
3. Normalized Mantissa: 가수(mantissa)는 실질적인 데이터를 의미합니다. 부호와 지수가 어떻든 간에 실수 표현법에서 의미있는 수는 mantissa가 표현합니다. 이 때, mantissa를 다음과 같이 정규화(normalize)합니다 (실수를 $F × r^E$ 으로 표기하는 과학적 표기법에서, $F$ 의 절대값이 1보다 같거나 크고 $r$ 보다 작은 $(1 ≤ |m| < r)$ 수가 되도록 표기하는 것을 정규화(normalized)된 과학적 표기법이라고 합니다):
  - mantissa를 1.xxx 형식으로 표현할 수 있도록 지수를 조정합니다.
  - 소수점 앞의 1은 항상 존재하므로 이 수는 mantissa를 표현할 때 (있다고 가정하고) 생략하고 소수점 뒤의 xxx부분만 표현합니다.

이를 그림으로 나타내면 다음과 같습니다:

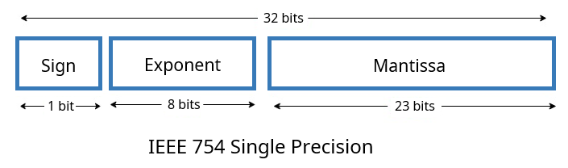
IEEE 754 single precision — IEEE 754 Single Precision (32 bits)

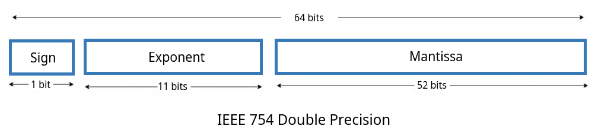
IEEE 754 double precision — IEEE 754 Double Precision (64 bits)

IEEE 754 floating_point_scheme — IEEE 754 부동소수점 scheme

이제 실수를 표현하는 예제를 살펴봅시다. 5.375를 예로 들면:

5.375 = 101.011₂ 입니다. 이를 다시 나타내면, 101.011₂ = 1.01011 × 2² 입니다.

mantissa는 01011이고, “unbiased” exponent는 2이므로 biased exponent는 2 + 127 = 129입니다. 따라서 5.375를 single precision으로 나타내면 다음과 같습니다:

0 10000001 01011000000000000000000

double precision은 biased exponent 부분만 제외하고 나머지는 동일합니다. double precision에서 biased exponent는 2 + 1023 = 1025입니다. 따라서 5.375를 double precision으로 나타내면 다음과 같습니다:

0 10000000001 0101100000000000000000000000000000000000000000000000

5.375는 컴퓨터로 정확하게 5.375라고 나타낼 수 있지만, 1.23과 같은 수는 정확하게 나타낼 수 없어 “근사”를 하여 나타냅니다. 1.23을 single precision으로 나타내면 다음과 같습니다 (double precision도 상황은 동일합니다):
0 01111111 00111010111000010100100

하지만 이는 실제로 1.23이 아니라 1.230000019073486328125입니다.

single precision과 double precision의 표현 범위를 나타내면 표로 나타내면 다음과 같습니다:

구분	범위	십진법 근사값	*유효 자리수
Single Precision	± $2^{-126}$ ~ $(2-2^{-23})×2^{127}$	± 약 $10^{-44.85}$ ~ $10^{38.53}$	약 6자리
Double Precision	± $2^{-1022}$ ~ $(2-2^{-52})×2^{1023}$	± 약 $10^{-323.3}$ ~ $10^{308.3}$	약 15 자리

*부동 소수점 표현 방식에서 값은 항상 정규화되어 표현되므로, mantissa의 정밀도에 따라 유효자리가 결정됩니다. Single precision의 경우, $1/2^{23}$ 까지 표현할 수 있으므로 최대 유효자리수는 약 $log(2^{23}) \simeq 6.923$ → 6자리이고, double precision의 경우 $1/2^{52}$ 까지 표현할 수 있으므로 최대 유효자리수는 약 $log(2^{52}) \simeq 15.653$ → 15자리입니다. 이는 시스템/컴파일러마다 차이가 있을 수 있습니다.

특수값 (Special Values)

특수값은 (+∞), (-∞), NaN을 표현할 때 사용됩니다. Exponent 비트가 모두 1일때:

mantissa 비트가 모두 0이면 무한대를 나타냅니다. 이 때 부호에 따라 +무한대, -무한대로 나뉩니다.
mantissa 비트가 모두 0이 아니면 NaN(Not a Number)를 나타냅니다. NaN은 연산 과정에서 잘못된 입력을 받았음을 나타내는 기호입니다.

비정규화된값 (Denormalized Values)

비정규화된값은 Exponent가 모두 0으로 채워진 경우를 의미합니다. 0을 표현하거나 매우 작은 소수점을 표현할 때 사용됩니다. 이 경우, 앞서 살펴본 정규화 방식에서는 소수점 앞에 1이 있다고 가정하였지만, 이 방법에서는 0.xxx이라고 가정하고 표현합니다.