병합 정렬

📢

• 여기서 소개하는 정렬은 오름차순정렬을 기준으로 합니다.
• n개의 원소를 저장하는 배열A를 A[0 ⋯ n - 1]라고 표현하겠습니다.

개념

병합 정렬은 주어진 배열을 반으로 나눈다음, 이렇게 나뉘어진 두 배열을 각각 독립적으로 정렬한 뒤 다시 합치는 과정을 수행하는 정렬 알고리즘 입니다. 자신보다 크기가 절반인 문제를 두 개 푼 다음 병합하는 과정을 재귀적으로 반복한다고 할 수 있습니다.

---

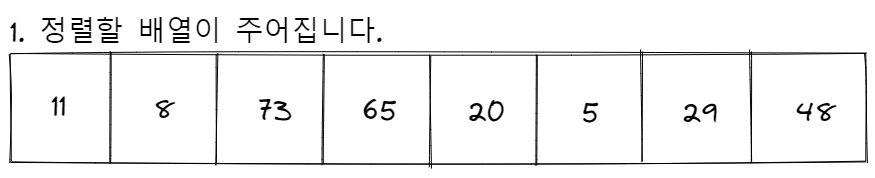
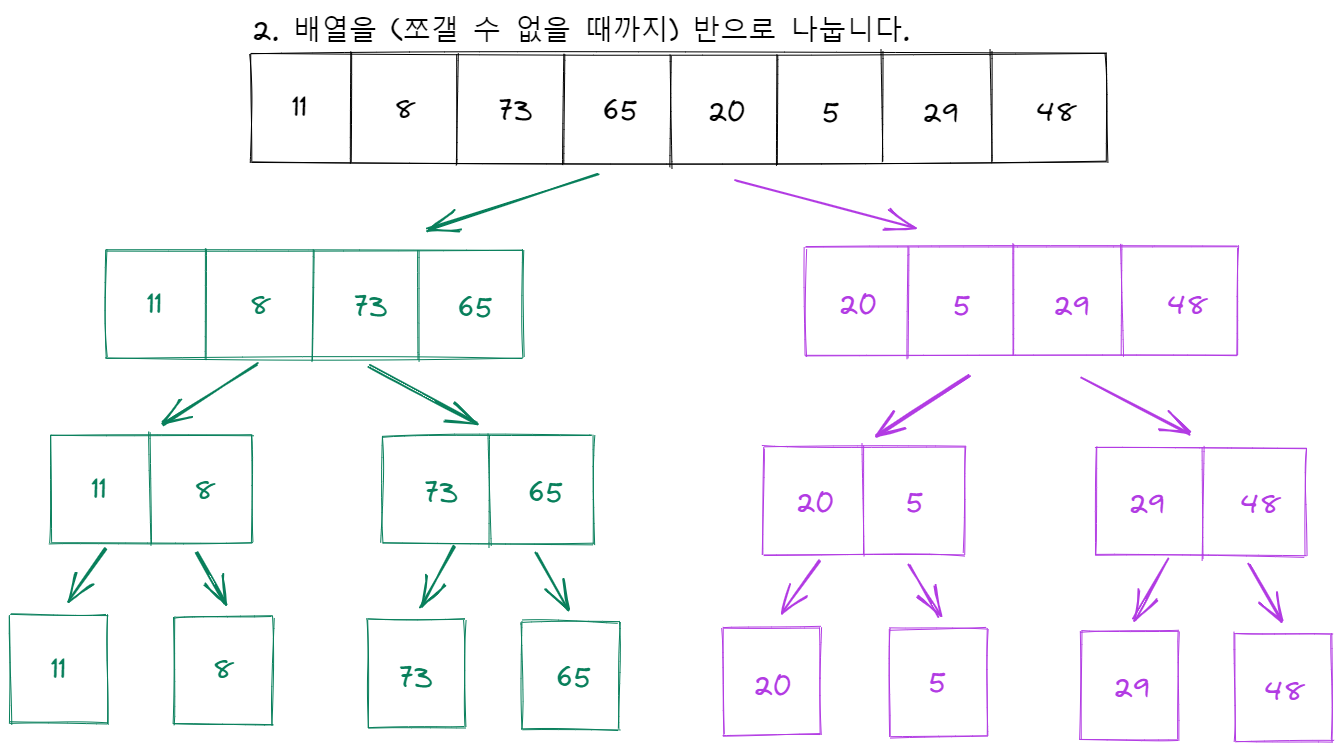
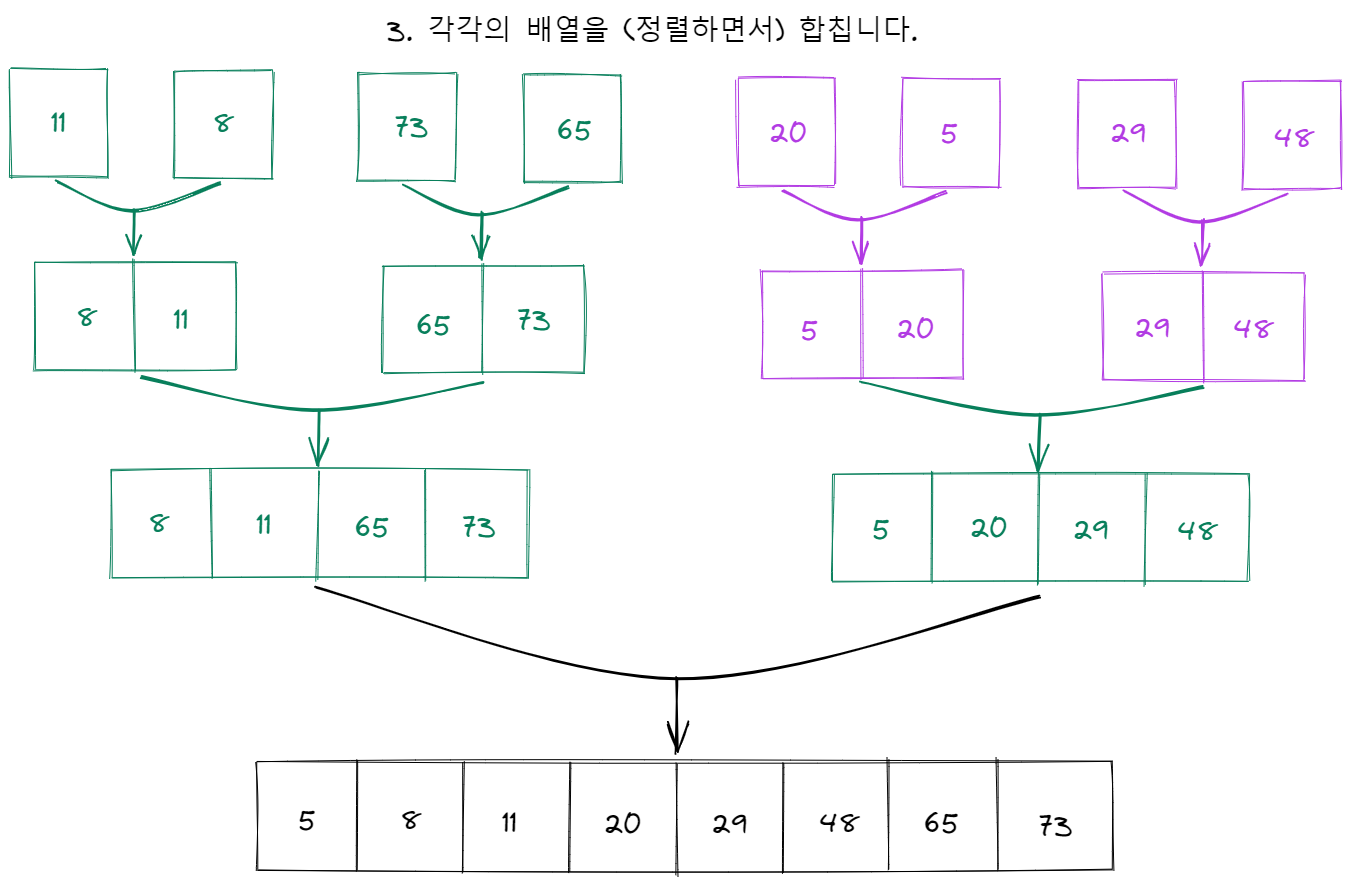
병합 정렬의 수행시간을 살펴봅시다. 크기가 n인 배열을 병합 정렬로 처리하는 시간은 다음과 같이 쓸 수 있습니다:

$T(n) ≤ \begin{cases} a &if\ n = 1\\ 2T(\frac{n}{2}) + cn &if\ n > 1 \end{cases}$

이 때 상수 a는 크기가 1인 문제를 푸는 시간을 나타내고, 상수 c는 병합에 드는 시간을 충분히 잡아주기 위해 곱합니다. 비교 횟수만으로 수행 시간을 분석한다면 c = 1로도 충분합니다. 어쨌든 병합에는 선형 시간이 소요됩니다.

여기서 $T(\frac{n}{2})$는 두 개의 작은 문제를 처리하는 비용, 즉 재귀 호출과 관련된 것입니다.

$n = 2^k$,(k는 음이 아닌 정수)라 가정하고 이를 전개하면 다음과 같습니다. 이 때 $logn$은 $log_2n$을 의미합니다:

$T(n) ≤ 2T(\frac{n}{2}) + cn$
          $≤ 2(2T(\frac{n}{4}) + c\frac{n}{2}) + cn = 2^2T(\frac{n}{2^2}) + 2cn$
          $≤ 2^2(2T(\frac{n}{2^3})+c\frac{n}{2^2}) + 2cn = 2^3T(\frac{n}{2^3})+3cn$
          $...$
          $≤ 2^kT(\frac{n}{2^k}) + kcn$
          $=nT(1)+kcn = an+cnlogn$
          $=nT(1)+kcn = an+cnlogn$
          $=Θ(nlogn)$

혹은, 마스터 정리를 이용해서 바로 수행시간을 알아낼 수도 있고, 점화식을 $T(n)=2T(\frac{n}{2})+Θ(n)$으로 표현할 수도 있습니다 (이 경우에도 마스터 정리를 이용해서 바로 알아낼 수 있습니다).

구현 코드

구현 코드 보러가기