삽입 정렬

📢

• 여기서 소개하는 정렬은 오름차순정렬을 기준으로 합니다.
• n개의 원소를 저장하는 배열A를 A[0 ⋯ n - 1]라고 표현하겠습니다.

개념

삽입 정렬은 이미 정렬되어 있는 길이가 i인 배열에 하나의 원소를 더해서, 길이가 i + 1인 정렬된 배열을 만드는 과정을 반복합니다. 선택 정렬과 버블 정렬이 n개 짜리 배열에서 시작하여 그 크기를 하나씩 줄여나가는데 반해, 삽입 정렬은 한 개짜리 배열에서 시작하여 그 크기를 하나씩 늘려가는 정렬이라고 볼 수 있습니다.

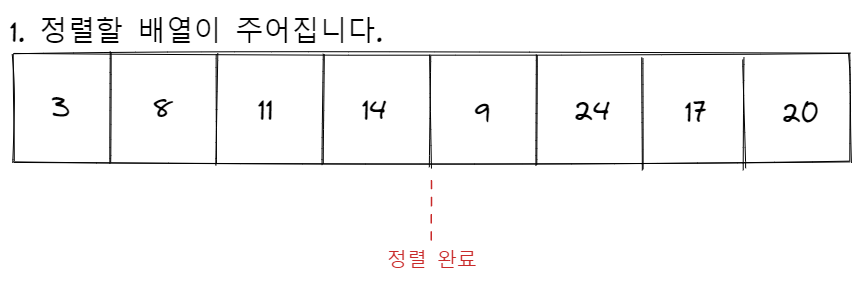
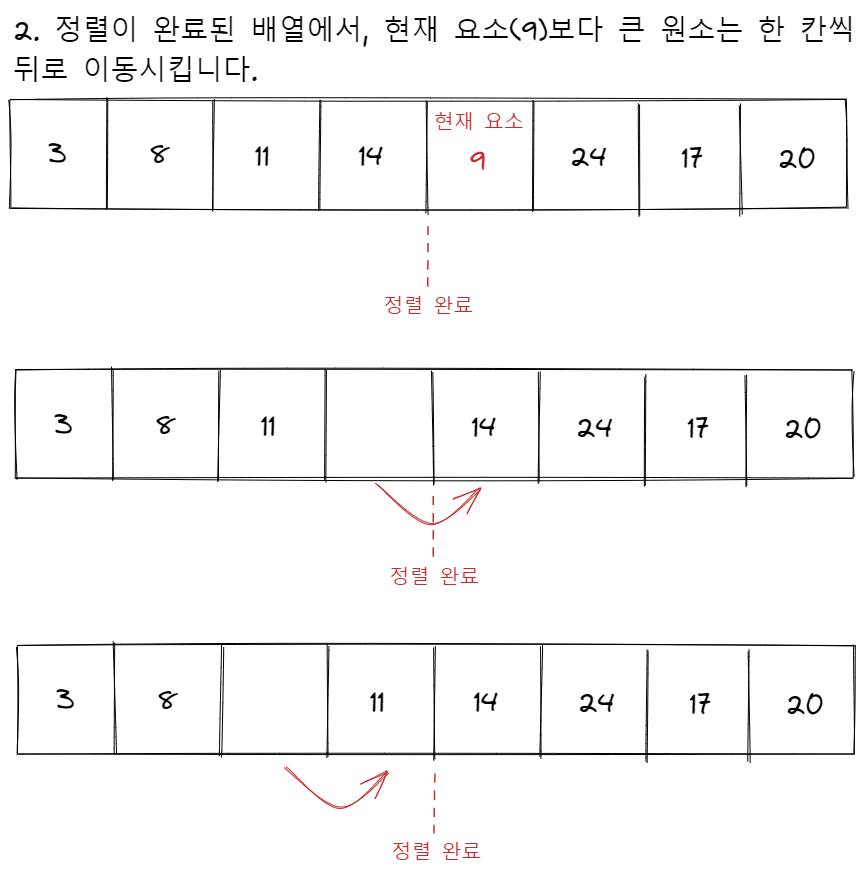
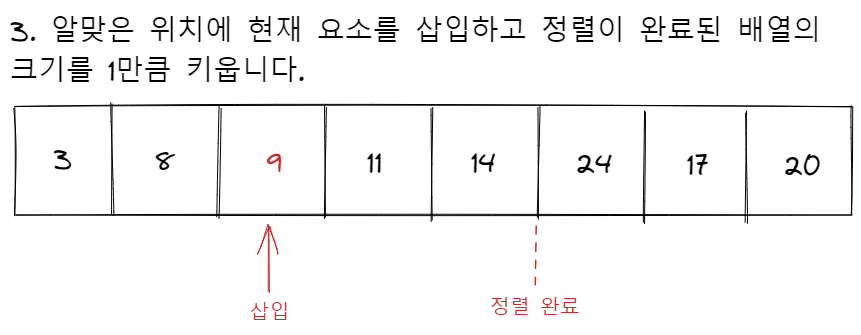
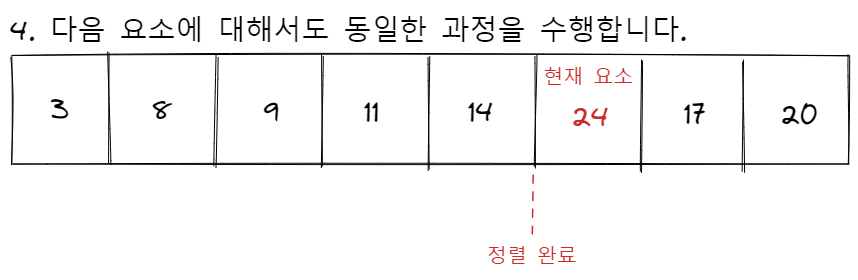
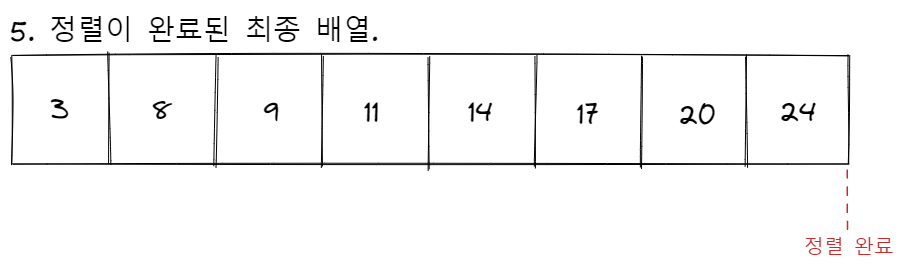
삽입 정렬은 $O(n^2)$시간이 소요되는 비효율적인 정렬 알고리즘에 속하지만, 거의 정렬되어 있는 배열이 입력으로 들어오는 경우 가장 매력적인 알고리즘이 됩니다. 배열이 완전히 정렬된 채로 입력된다면 현재 요소를 삽입할 위치를 탐색하는 루프는 한 번도 수행되지 않게되므로 $Θ(n)$의 시간이 소요됩니다.

배열의 거의 정렬되어 있을 경우에도 현재 요소의 삽입이 수월해져서 $Θ(n)$에 가까운 시간이 소요됩니다.

버블 정렬에서 이런 무의미한 반복을 없애기 위한 (sorted와 같은)특별한 장치를 소개했지만, 이 경우 여분의 코드 때문에 오버헤드가 발생할 수 있습니다. 이에 반해 삽입 정렬은 아무런 장치 없이 효율적으로 끝나게 되는데, 이러한 매력 때문에 상황에 따라 가끔씩 삽입 정렬을 섞어서 쓰는 경우도 존재합니다.

---

앞서 언급했듯이, 선택 정렬과 버블 정렬은 n개 짜리 배열에서 시작하여 아직 정렬되지 않은 배열의 크기를 하나씩 줄여나가는반면, 삽입 정렬의 경우 1개 짜리 배열에서 시작하여 이미 정렬된 배열의 크기를 하나씩 늘려가는 정렬입니다.

삽입 정렬에는 귀납법의 원리가 그대로 스며있는데, 먼저 배열의 크기가 1일때는 “성립”합니다 (즉, 정렬됩니다). 배열의 크기가 k일 때 성립하면(정렬되어 있으면), 요소를 적절한 위치에 삽입함으로써 크기가 k + 1일 때에도 성립하게 됩니다.

선택 정렬과 버블 정렬도 수학적 귀납법으로 증명할 수 있지만, 이 중에서 선택 정렬의 귀납적 성질이 가장 선명에게 나타난다고 할 수 있습니다.

구현 코드

구현 코드 보러가기