이진 탐색

이진 탐색이란?

어떤 그룹 내에 존재하는 요소를 찾고자 할 때, 가장 일반적인 방법은 해당 그룹의 요소를 하나하나 살펴보는 것입니다. 이를 선형 탐색(linear search)라고 하는데, 이러한 알고리즘은 O(n)의 시간복잡도를 갖습니다.

이때 그룹 내의 요소들이 일정한 순서로 정렬되어 있다면 이진 탐색(binary search) 기법을 활용할 수 있습니다. 이진 탐색의 기본 아이디어는 일정 범위에 대해, 범위의 중간 부분에 찾고자 하는 요소가 있는지 확인하고 만약 없다면 현재 살펴보고 있는 요소를 기준으로 검색 범위를 절반씩 줄여나가는 것입니다.

숫자가 저장된 배열을 예로 들면 다음과 같습니다. (이미지 출처):

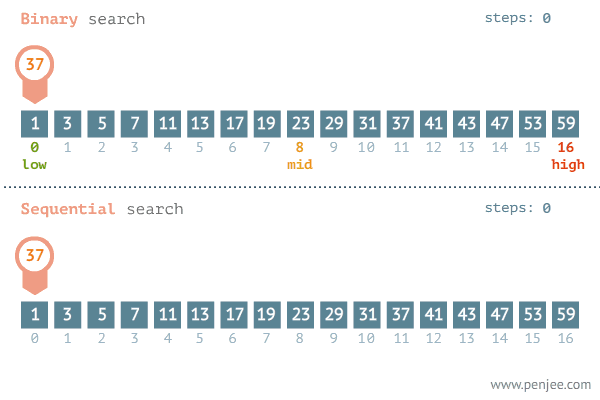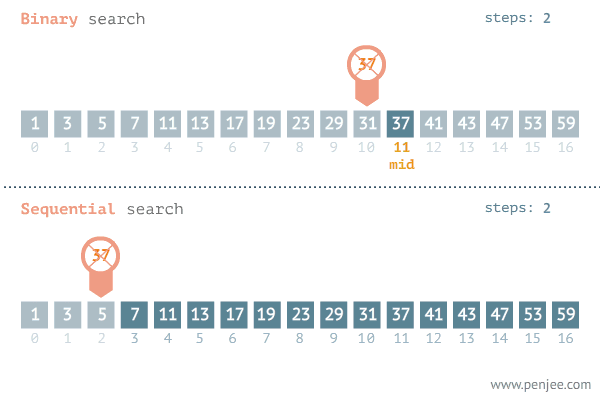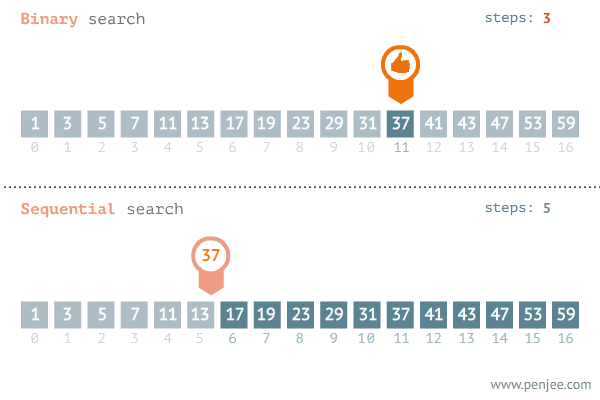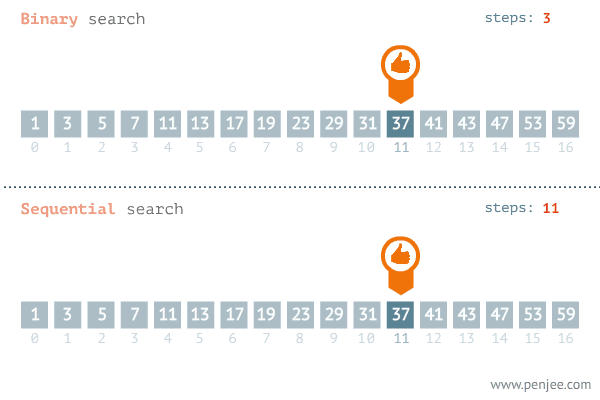
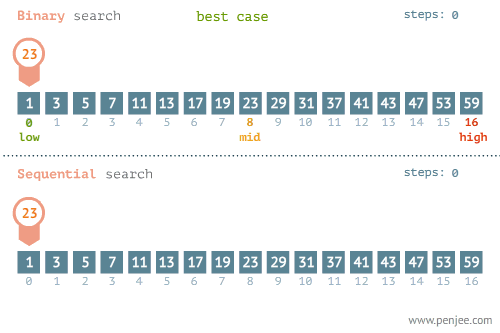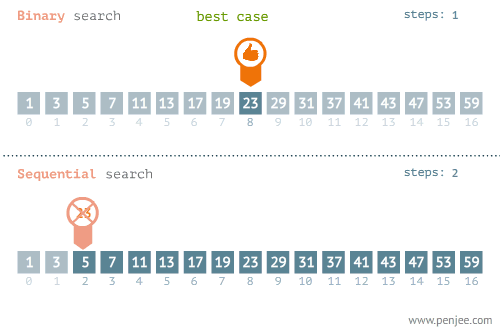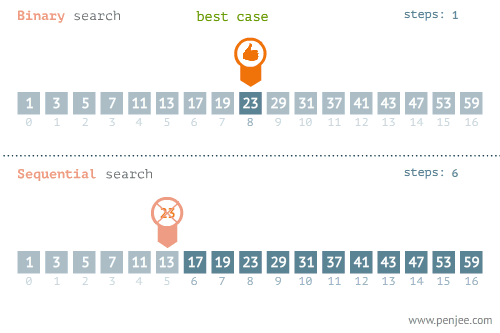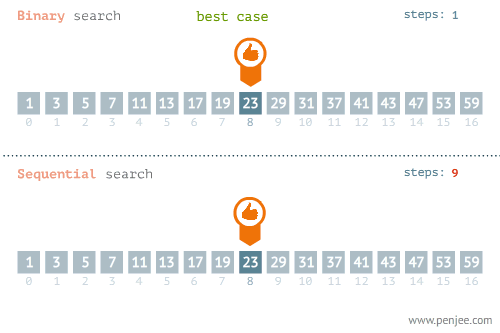
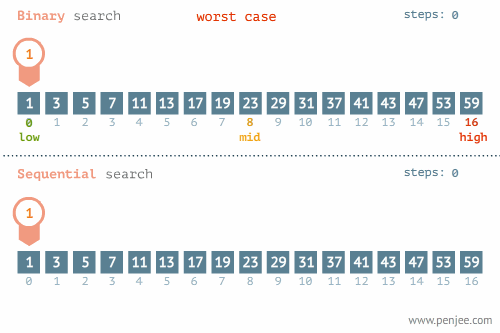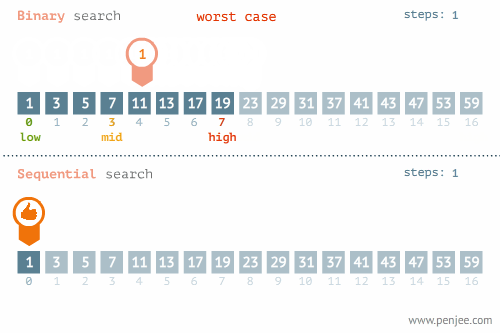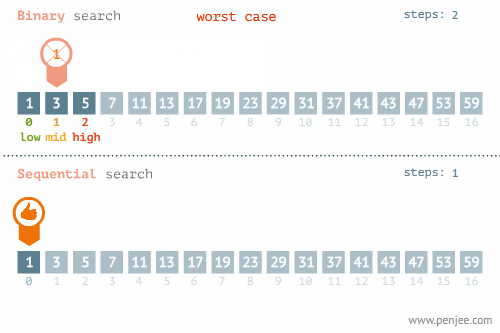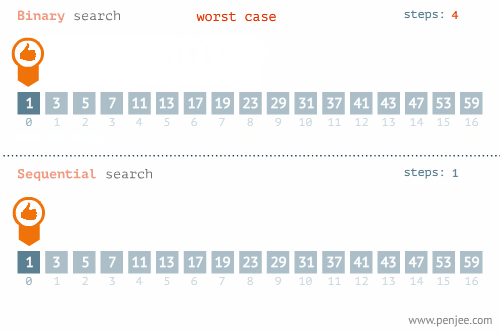
이처럼 현재 살펴보고 있는 요소와 우리가 찾고자 하는 요소가 같은지를 검사할 때마다 탐색 범위를 절반씩 줄여나가기 때문에 일반적으로 선형 탐색보다 성능이 훨씬 뛰어납니다. 이진 탐색의 시간 복잡도는 O(log n) 입니다.

구현

📌 배열의 모든 요소가 숫자이고, 오름차순으로 정렬된 배열을 예시로 들겠습니다.

탐색 범위

이진 탐색은 일정 범위를 설정한 뒤 범위를 계속 좁혀나가는 방식으로 원하는 값을 찾아나간다고 볼 수 있습니다. 왼쪽 경계를 lo, 오른쪽 경계를 hi라고 한다면, 일반적인 상황에서 초기 범위는 배열 전체가 될 것입니다:

let lo = 0;
let hi = arr.length - 1;

mid

이렇게 찾고자 하는 범위가 설정되면, 해당 범위의 중간에 오는 요소를 살펴봅니다. 일반적으로 중간 요소의 인덱스를 다음과 같이 구할 수 있을 것입니다:

const mid = Math.floor((lo + hi) / 2); // 범위안에 요소가 짝수개 있는 경우, 중간 값 후보 2개 중 왼쪽 요소를 선택
const mid = Math.floor((lo + hi + 1) / 2); // 범위안에 요소가 짝수개 있는 경우, 중간 값 후보 2개 중 오른쪽 요소를 선택

하지만 중간 요소의 인덱스를 위와 같이 구하게 되면, 인덱스가 매우 클 때 오버플로우가 발생할 수 있습니다. 이를 방지하기 위해 아래와 같은 방법을 사용할 수 있습니다:

// 훨씬 낫긴 합니다만 여전히 오버플로우가 발생할 가능성이 있습니다.
const mid = lo + Math.floor((hi - lo) / 2);

// 가장 좋은 방법입니다만 한눈에 이해하기 어려울 수 있습니다.
const mid = (lo + hi) >>> 1;

(물론 자바스크립트에선 정확하게 표현할 수 있는 정수값이 $2^{53}-1$인데 반해, 배열의 최대 길이가 $2^{32}-1$이므로 오버플로우가 발생할 가능성은 없다고 할 수 있을 것 같습니다.)

범위 줄여나가기

범위의 중간 인덱스를 구했으면 해당 인덱스의 요소와 우리가 찾고자 하는 요소를 비교할 차례입니다. 오름차순으로 정렬된 배열이라고 가정하고, 중간 요소를 mid, 찾고자 하는 요소를 target이라 한다면 다음과 같이 범위를 줄여나갈 수 있습니다:

// mid === target인 경우 우리가 찾고자 하는 요소를 찾은 것이므로
// 해당 인덱스를 반환하고 알고리즘을 종료하면 됩니다.
if (arr[mid] === target) return mid;

// mid < target인 경우 중간 요소를 포함하여 왼쪽에 있는 요소들은 살펴볼 필요가 없게 됩니다.
// 따라서 이 경우 왼쪽 경계를 mid + 1 인덱스로 당깁니다.
if (arr[mid] < target) lo = mid + 1;

// mid > target인 경우 중간 요소를 포함하여 오른쪽에 있는 요소들은 살펴볼 필요가 없게 됩니다.
// 따라서 이 경우 오른쪽 경계를 mid - 1 인덱스로 당깁니다.
if (arr[mid] > target) hi = mid - 1;

위와 같은 방법을 사용하여 범위를 절반씩 줄여나갈 수 있습니다. 내림차순의 경우 위와 반대로 하면 되겠죠.

언제까지 탐색?

그럼 도대체 언제까지 탐색을 해나가야 할까요? 바로 범위의 크기가 1, 즉 lo === hi가 될때까지 탐색을 해나가면 됩니다:

while(lo <= hi) { /* ... */ }

계속해서 범위를 줄여나가다가 lo > hi가 되는 순간 탐색을 마치고 값을 찾지 못했다는 의미로 -1 등을 반환할 수 있습니다. 왼쪽 경계가 오른쪽 경계보다 더 커졌다는 말은 최초에 주어진 범위를 모두 탐색하였으나 값을 찾지 못했다는 뜻이니까요!

구현 코드

구현 코드 보러가기