알고리즘 분석

알고리즘 분석이란?

알고리즘 분석이란, 알고리즘의 자원(resource) (실행 시간, 메모리, 통신 등등..) 사용량을 분석하는 것을 의미합니다.

시간복잡도 (Time Complexity)

알고리즘의 실행 시간은 실행환경 (컴퓨터의 성능, 운영체제, 프로그래밍 언어, 컴파일러 등)에 따라 달라질 수 있습니다. 이로 인해 알고리즘의 “정확한” 실행 시간을 측정하여 비교하는 것은 사실상 불가능하므로, 대신 알고리즘이 수행하는 연산의 실행 횟수를 세어 알고리즘을 분석합니다.

이때, 연산의 실행 횟수는 입력 데이터의 크기에 관한 함수로 표현하게 되는데, 데이터의 크기가 같더라도 실제 데이터(이를테면 데이터의 종류)에 따라서 달라질 수 있습니다.

점근 표기법 (Asymptotic Notation)

점근 표기법은 데이터의 크기(개수)가 무한대를 향한다 (n → ∞)라고 했을 때, 그에 따라 수행 시간이 증가하는 비율 (growth rate)로 시간복잡도를 표현하는 방법입니다. 흔히 사용되는 표기법에는 빅 오 (Big-O Notation), 빅 오메가(Big-Ω Notation), 빅 세타(Big-Θ Notation)이 있습니다.

이 분석 방법은 유일한 분석법도 아니고 가장 좋은 분석법도 아니지만, 상대적으로 간단하며 알고리즘 실행환경에 비의존적(independent)이므로 가장 광범위하게 사용되는 분석법입니다.

• Big-O 표기법: 수행 시간의 상한선을 표현합니다. 예를 들어, 길이가 n인 배열의 모든 원소를 한 번씩 순차적으로 프린트하는 알고리즘을 흔히 O(n) 으로 표기하지만, O(n2), O(n3), O(2n)으로 표현할 수 도 있습니다. 즉, 시간 복잡도를 Big-O로 표현하면 “알고리즘이 적어도 이 정도 빠르기로 동작한다” 라고 표현하는 것과 같습니다.
• Big-Ω 표기법: Big-O 표기법과 비슷하지만, Big-Ω의 경우 상한선이 아닌 하한선을 의미합니다. Big-O에서 들었던 예의 경우, Ω(n)으로 표현할 수도 있고, Ω(log n), 혹은 Ω(1)로 표현할 수 있습니다. 즉, “알고리즘이 이것보단 빠르게 동작하지는 않는다” 라고 표현하는 것입니다.
• Big-Θ 표기법: Big-Θ 표기법은 Big-O와 Big-Ω를 둘 다 만족하는 경우라고 볼 수 있습니다. 즉, 어떤 알고리즘이 O(n) 이고 Ω(n) 이면 Θ(n) 입니다.

흔히 알고리즘의 수행시간을 분석할 때 Big-O를 사용하는데, 그 이유는

• Big-Ω의 경우, 알고리즘 수행 시간의 하한선, 즉 “이것보단 빠를 수 없다”를 나타내는데, 이는 대개 유용하지 않습니다. 보통 우리는 알고리즘이 “제일 느리게 동작할 때는 어느 정도로 동작하는지”에 관심이 있기 때문입니다. 알고리즘이 느리게 동작하는 것이 문제이지 빠르게 동작하는 게 문제인 경우는 사실상 없으니까요!
• Big-Θ의 경우 상한, 하한의 개념이 아니라 실행 시간에 대해 “근접한 한계값(tight bound)“이 있다고 표현하는 것입니다. 하지만 이 “근접한 한계값”을 구하는 게 상한을 구하는 것보다 어려울 수 있고, 실제로 알고리즘을 분석할 때 대게 실행 시간의 “상한”에 관한 정보로도 충분하기 때문입니다.

Big-O 표기 예시

Big-O로 시간 복잡도를 표현할 때는 최고차항만을 표기하며, 상수항은 무시합니다. 예를 들어, 입력 데이터 n에 대해 12n2+ 4n + 7 만큼 연산을 수행하는 함수가 있다고 한다면 이 함수의 시간 복잡도는 최고차항인 12n2만을 고려하며 특히 이 중에서도 상수항을 제외한 n2 만을 고려합니다. 따라서 이 함수의 시간복잡도는 O(n2)이 됩니다.

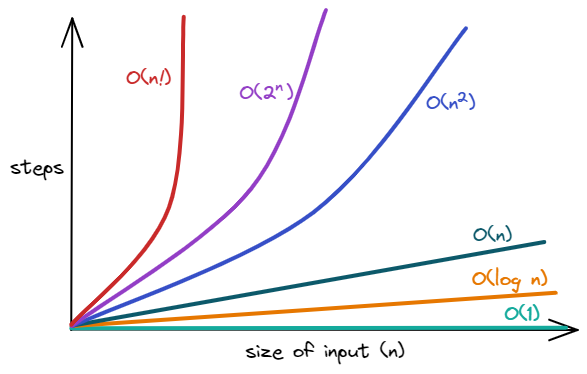
대표적인 Big-O 표기법의 종류는 다음과 같습니다:

• O(1): 입력값에 관계없이 실행 시간이 일정한, 최고의 알고리즘 이라 할 수 있습니다. 하지만 만약 상수값이 매우 매우 크다면 사실상 일정한 실행 시간의 의미가 없을 수 있습니다. 최고의 알고리즘이 될 수 있지만, 그만큼 신중해야 합니다. 알고리즘의 예시로는 인덱스를 통한 배열 요소 접근 (arr[1])이 있습니다.
• O(log n): 입력값 n에 대해 시간이 log n의 비율로 증가합니다. 일반적으로 로그의 밑(base)은 2를 사용합니다. 대표적인 예로는 이진 탐색이 있습니다.
• O(n): 입력값 n에 대해 선형적으로 시간이 증가합니다. 즉, 수행 시간이 입력값에 비례한다고 할 수 있습니다. 정렬되지 않은 배열에서 최대값 혹은 최소값을 찾는 경우가 이에 해당합니다.
• O(n log n): 병합 정렬을 비롯한 대부분의 효율이 좋은 정렬 알고리즘이 이에 해당합니다.
• O(n²): 버블 정렬 같은 비효율적인 정렬 알고리즘이 이에 해당합니다.
• O(2ⁿ): 피보나치 수를 재귀적으로 계산하는 알고리즘이 이에 해당합니다.
• O(n!): 외판원 문제 (TSP)를 브루트 포스로 풀 경우 이에 해당합니다. 입력값이 조금만 커져도 수행 시간이 무자비하게 증가하게 됩니다.

number of n	n	n log n	n2	n3	2n	n!
n=10	< 1 sec	< 1 sec	< 1 sec	< 1 sec	< 1 sec	4 sec
n=30	< 1 sec	< 1 sec	< 1 sec	< 1 sec	18 min	1025 years
n=50	< 1 sec	< 1 sec	< 1 sec	< 1 sec	36 years	very long
n=100	< 1 sec	< 1 sec	< 1 sec	1 sec	1017 years	very long
n=1,000	< 1 sec	< 1 sec	1 sec	18 min	very long	very long
n=10,000	< 1 sec	< 1 sec	2 min	12 days	very long	very long
n=100,000	< 1 sec	2 sec	3 hours	32 years	very long	very long
n=1,000,000	1 sec	20 sec	12 days	31, 710 years	very long	very long

공간 복잡도 (Space Complexity)

지금까지는 시간 복잡도를 표현하는 방법에 대해 알아보았는데, Big-O는 시간 복잡도 외에도 공간 복잡도를 표현하는 데에도 널리 쓰입니다. 즉, 시간 복잡도에서와같이 입력값 n에 대해 공간 복잡도가 O(n)이면 해당 알고리즘은 입력값에 비례하여 메모리를 사용한다는 뜻이 됩니다.

또, 알고리즘은 흔히 “시간과 공간이 trade-off” 관계에 있다고 하는데, 즉 실행 시간이 빠른 알고리즘은 그만큼 공간(메모리)를 많이 사용하고, 반대로 공간을 적게 사용하는 알고리즘은 그만큼 실행 시간이 느리다는 뜻입니다. 물론 실행 시간이 빠르면서도 공간을 적게 사용하는 알고리즘이 있긴 하지만, 대부분의 경우 시간과 공간은 trade-off 관계에 있다고 할 수 있습니다.